Архив по дате: Июль - 2015

119971. Найдите количество точек
119971.На рисунке изображен график функции f(x), определенной на интервале (–5;5). Найдите количество точек, в которых производная функции f(x) равна 0.
119971.На рисунке изображен график функции f(x), определенно...
На рисунке изображен график производной
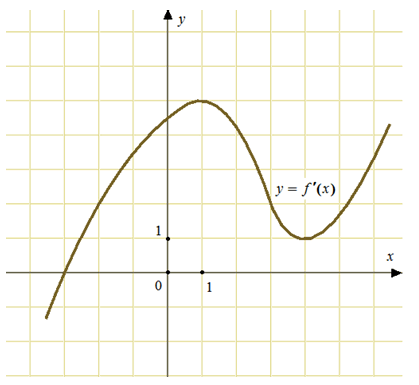
40131. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна оси абсцисс или совпадает с ней.
40131. На рисунке изображен график у=f′(x) - производной фун...
Найдите абсциссу точки, в которой касательная
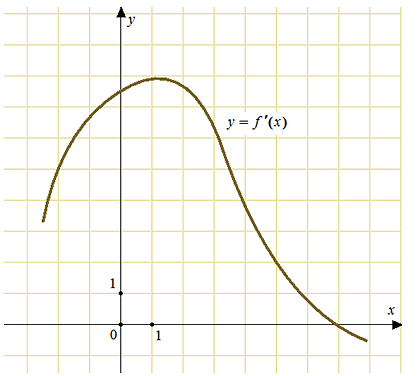
40130. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна прямой у = 2х–2 или совпадает с ней.
40130. На рисунке изображен график у=f′(x) — производной фун...
На рисунке изображен график
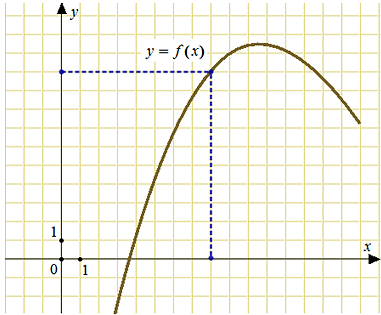
40129. На рисунке изображен график функции у=f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 8. Найдите значение производной функции в точке х0=8.
40129. На рисунке изображен график функции у=f(x). Прямая, п...
27506. Найдите значение производной
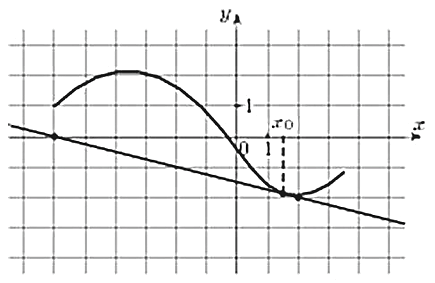
27506. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
27506. На рисунке изображены график функции у=f(x) и касател...
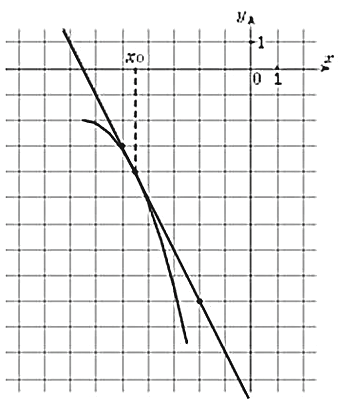
27505. Найдите значение производной
27505. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
27505. На рисунке изображены график функции у=f(x) и касател...
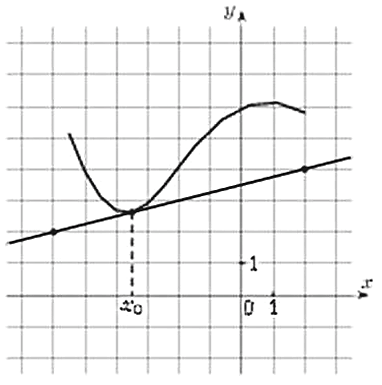
27504. Найдите значение производной
27504. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
27504. На рисунке изображены график функции у=f(x) и касател...
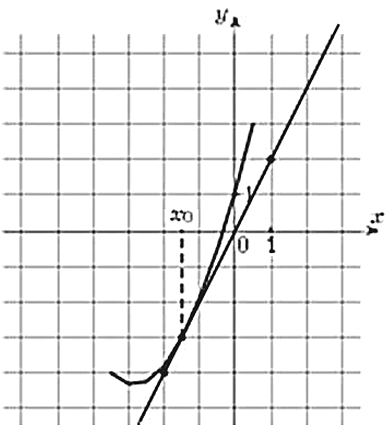
27503. Найдите значение производной
27503. На рисунке изображены график функции у=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.
27503. На рисунке изображены график функции у=f(x) и касател...

Найдите точку экстремума функции f(x)
27502. На рисунке изображен график у=f′(x)— производной функции f(x), определенной на интервале (–4;8). Найдите точку экстремума функции f(x), принадлежащую отрезку [–2;6].
27502. На рисунке изображен график у=f′(x)— производной функ...

Найдите количество точек
27501. На рисунке изображен график у=f′(x)— производной функции f(x), определенной на интервале (–10;2). Найдите количество точек, в которых касательная к графику функции f(x) параллельна прямой у= –2х–11 или совпадает с ней.
27501. На рисунке изображен график у=f′(x)— производной функ...


