40131. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна оси абсцисс или совпадает с ней.
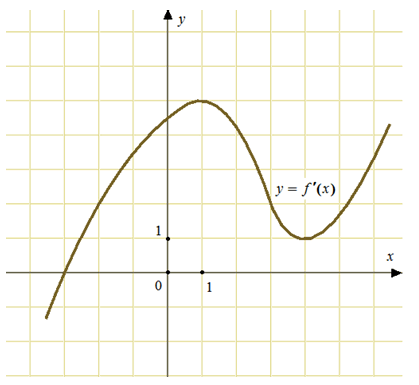
Касательная к графику у=f(x) может быть параллельна оси абсцисс или совпадать с ней, только в точках, где производная равна нулю (это могут быть точки экстремума или стационарные точки (в окрестностях которых производная свой знак не меняет). По данному графику видно, что производная равна нулю только в одной точке х=–3.
Можно построить рассуждение следующим образом:
Значение производной в точке касания равно угловому коэффициенту касательной. Поскольку касательная параллельна оси абсцисс или совпадает с ней, её угловой коэффициент равен 0 (действительно тангенс угла в ноль градусов равен нулю).
Следовательно, мы ищем точку, в которой угловой коэффициент, равен нулю, а значит, и производная равна нулю. Производная равна нулю в той точке, в которой её график пересекает ось абсцисс. Поэтому искомая точка х=–3.
Ответ: –3



