40130. На рисунке изображен график у=f′(x) — производной функции f(x). Найдите абсциссу точки, в которой касательная к графику у=f(x) параллельна прямой у = 2х–2 или совпадает с ней.
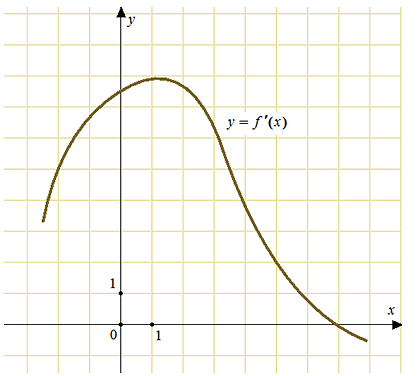
Значение производной в точке касания равно угловому коэффициенту касательной. Так как касательная параллельна прямой у = 2х–2 или совпадает с ней, она имеет такой же угловой коэффициент равный 2 и значит f′(x0) = 2.
Осталось найти, при каких x производная принимает значение 2. Графически это точка пересечения графика производной с прямой f′(x0) = 2
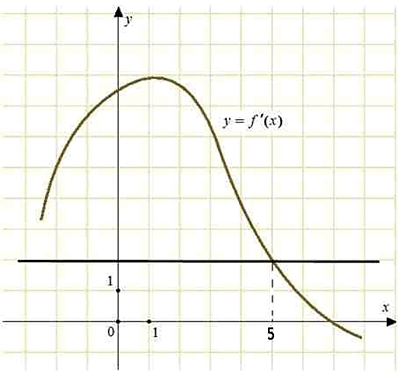
Искомая точка x0 = 5
Ответ: 5



