Прямая у=–5х+8 является касательной

119973. Прямая у=–5х+8 является касательной к графику функции 28х²+bх+15. Найдите b, учитывая, что абсцисса точки касания больше 0.

График заданной функции — парабола. Прямая с параболой имеет  единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение

28х²+bх+15=–5х+8 имело единственно решение:

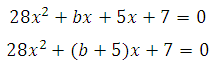
Квадратное уравнение будет иметь единственное решение тогда, когда дискриминант будет равен нулю:

Теперь определим при каком значении абсцисса точки касания будет больше нуля, подставляем оба значения в 28х²+(b+5)х+7=0. Подставляем поочерёдно:

Таким образом,  искомое значение b=–33 (при этом значении абсцисса точки касания положительна).

Другой способ:

Условия касания графика функции y=f(x) и прямой y=kx+b задаётся системой требований:

В нашем случае получаем:

По условию, абсцисса точки касания положительна, значит x=0,5

Ответ: −33