27450. Найдите тангенс угла АОВ, построенного на листке в клетку.
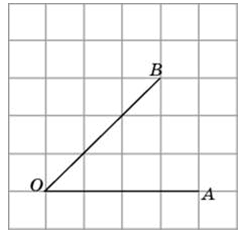
По эскизу видно, что угол АОВ равен 45 градусам. Известно, что тангенс 45 градусов равен 1 (табличное значение).
*Ещё способ. Найдём тангенс заданного угла используя определение. Проведём перпендикуляр BD к ОА, тогда BD=OD=3.

Рассмотрим треугольник BDО – он прямоугольный и равнобедренный. Известно, что тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему, значит:
![]() Ответ: 1
Ответ: 1
27459. Найдите тангенс угла AOB.

Соединяем точки А и В:

Получили треугольник АОВ.
Найдём все стороны треугольника. Это можно сделать используя теорему Пифагора. Далее используя теорему косинусов, найдём косинус угла, а затем тангенс.
Итак, АВ = 5. Отрезок ОВ это гипотенуза в прямоугольном треугольнике с катетами 1 и 2, следовательно:![]()
Отрезок OА это гипотенуза в прямоугольном треугольнике с катетами 1 и 3, следовательно:
![]()
По теореме косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.

Из основного тригонометрического тождества найдём sin AOB:

Ответ: –1



