27261. В прямоугольном треугольнике АВС угол С равен 900, АВ=4√15, sinA=0,25. Найдите высоту СН.
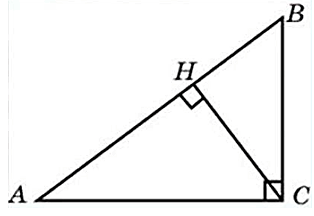В подобных задачах такие элементы, как СН, АН, ВН можно найти используя основное тригонометрическое тождество и определения синуса, косинуса, тангенса, котангенса.
Элементы СН, АН, ВН являются катетами прямоугольных треугольников. В подобных задачах элемент можно рассматривать в составе разных треугольников.
Рассмотрим треугольник АСН, по определению синуса:
Синус угла А известен, найдём АС. Рассмотрим треугольник АВС. По определению косинуса:
Найдём cosA Из основного тригонометрического тождества sin2A+cos2A=1 следует, что
Таким образом,
Значит CH=AC∙sinA=15∙0,25=3,75.
Ответ: 3,75
27265. Треугольник АВС прямоугольный, угол C равен 900, СН – высота, AB=13, tg A=0,2. Найдите АН.
Отрезок АН мы можем найти из треугольника . То есть необходимо найти какие-либо элементы в этом треугольнике. Так как известен tg A=0,2 то можно найти cosA.
Это значение потребуется для нахождения АС в треугольнике АВС. Зная АС и cos A в треугольнике АНС сможем найти АН. Итак, найдём cosA.
Из основного тригонометрического тождества sin2A+cos2A=1 делением левой и правой частей на cos2A получим:
Значит
Следовательно:
Рассмотрим треугольник АВС. По определению косинуса:
Теперь рассмотрим треугольник АНС. По определению косинуса:
Ответ: 12,5
27271. Треугольник АВС прямоугольный угол C равен 900, СН – высота, ВС=3, cos A =(√35)/6 Найдите АH.
Зная cos A можно найти tgA и sinA. Из основного тригонометрического тождества sin2A+cos2A=1 следует, что
Найдём тангенс угла А:
Рассмотрим треугольник ABC. По определению тангенса:
Рассмотрим треугольник ACH. По определению косинуса:
Ответ:17,5
