Прямая у=3х+1 является касательной

119972. Прямая у=3х+1 является касательной к графику функции ах²+2х+3. Найдите a.

Прямая и график  данной функции имеют одну общую точку, это значит, что данные уравнения можно внести для решения в одну систему, но этих уравнений будет недостаточно для решения.

Известно, что производная функции  в данной точке равна угловому коэффициенту касательной y=kx+b (k угловой коэффициент), то есть f′(x₀)=k. Это третье уравнение:

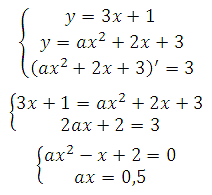
Подставим ax из второго уравнения в первое, получим:

Найдём а, подставим х=4  в  ах²–х+2=0:

Второй способ:

По смыслу задачи параметр  a≠0,  график заданной функции — парабола. Прямая с параболой имеет  единственную общую точку, так как сказано, что эта прямая является касательной. Поэтому необходимо и достаточно, чтобы уравнение ах²+2х+3=3х+1 имело единственное решение:

Квадратное уравнение будет иметь единственное решение, когда дискриминант будет равен нулю:

Ответ: 0,125