27132. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.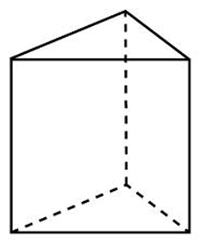 
Площадь поверхности призмы складывается из площадей всех граней, это два равных по площади основания и боковая поверхности. Найдём ребро пирамиды, являющееся гипотенузой прямоугольного треугольника, лежащего в основании. По теореме Пифагора:
Теперь можем найти площадь основания, площадь боковой поверхности. Площадь основания равна:
Площадь боковой поверхности призмы с периметром основания равна:
Полная площадь поверхности призмы:
Ответ: 288
27151. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.
Задача обратная предыдущей. Найдём ребро пирамиды, являющееся гипотенузой прямоугольного треугольника, лежащего в основании. По теореме Пифагора:Из общей площади поверхности вычитаем площади оснований:
Получили площадь боковой поверхности. Она равна произведению периметра основания на высоту:
Ответ: 10
27150. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.
Для вычисления боковой поверхности призмы воспользуемся формулой:
В данном случае боковое ребро это общее ребро перпендикулярных друг другу граней, оно равно 10. Перпендикулярным сечением призмы является прямоугольный треугольник с катетами 6 и 8. Найдём его гипотенузу и сможем вычислить периметр:
Таким образом:
Ответ: 240
*Комментарий: по-сути, вопрос стоит о нахождении суммы площадей параллелограммов. Понятно, что расстояние между ребрами 6 и 8 это высоты двух параллелограммов, а боковое ребро это основание. Мы нашли третью высоту грани и вычислили площадь.
Можно было записать сумму площадей граней так:
