Категория: Физические задачи

В ходе распада радиоактивного изотопа
27991. В ходе распада радиоактивного изотопа, его масса уменьшается по закону: mo— начальная масса изотопа t (мин) — прошедшее от начального момента время T — период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени mo…
27991. В ходе распада радиоактивного изотопа, его масса умен...

При адиабатическом процессе для идеального
27990. При адиабатическом процессе для идеального газа выполняется закон pVk=const, где p — давление в газе в паскалях, V — объем газа в кубических метрах. В ходе эксперимента с одноатомным идеальным газом (для него k = 5/3)…
27990. При адиабатическом процессе для идеального газа выпол...
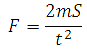
Автомобиль, масса которого равна
27989. Автомобиль, масса которого равна m=2160 кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь S=500 метров. Значение силы (в ньютонах), приложенной в это время к автомобилю,…
27989. Автомобиль, масса которого равна m=2160 кг, начинает ...

Для поддержания навеса планируется
27988. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле: m=1200 кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного…
27988. Для поддержания навеса планируется использовать цилин...

Скорость автомобиля, разгоняющегося
27987. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч , вычисляется по формуле v2=2la. Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от…
27987. Скорость автомобиля, разгоняющегося с места старта по...

На какое наименьшее количество ступенек
27986. Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до видимой им линии горизонта вычисляется по формуле Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. К пляжу ведет лестница, каждая ступенька…
27986. Расстояние от наблюдателя, находящегося на высоте h м...

На сколько метров нужно подняться
27985. Расстояние от наблюдателя, находящегося на высоте h м над землей, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле: Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку,…
27985. Расстояние от наблюдателя, находящегося на высоте h м...
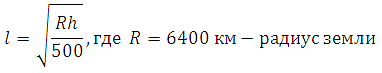
Расстояние от наблюдателя, находящегося
27984. Расстояние от наблюдателя, находящегося на небольшой высоте h метров над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле: На какой наименьшей высоте следует располагаться наблюдателю, чтобы он видел горизонт на расстоянии не…
27984. Расстояние от наблюдателя, находящегося на небольшой ...

При движении ракеты её видимая
27983. При движении ракеты её видимая для неподвижного наблюдателя длина, измеряемая в метрах, сокращается по закону: l0 = 5м — длина покоящейся ракеты с = 3∙105 км/с — скорость света …
27983. При движении ракеты её видимая для неподвижного наблю...

Скорость автомобиля, разгоняющегося с места
27982. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч2, вычисляется по формуле: Определите наименьшее ускорение, с которым должен двигаться автомобиль, чтобы, проехав один километр, приобрести скорость…
27982. Скорость автомобиля, разгоняющегося с места старта по...


